Ce înseamnă proiectarea unui vector pe axele de coordonate. Proiecția forței pe axă. Proiecția sumei vectoriale a forțelor pe axă. Teoreme de proiecție vectorială

O descriere vectorială a mișcării este utilă, deoarece într-un desen puteți descrie întotdeauna mulți vectori diferiți și puteți obține o „imagine” clară a mișcării în fața ochilor dumneavoastră. Cu toate acestea, este foarte consumator de timp să folosiți o riglă și un raportor pentru a efectua operații cu vectori de fiecare dată. Prin urmare, aceste acțiuni sunt reduse la acțiuni cu numere pozitive și negative - proiecții de vectori.

Proiecția vectorului pe axă numiți o valoare scalară egală cu produsul dintre modulul vectorului proiectat și cosinusul unghiului dintre direcțiile vectorului și axa de coordonate selectată.

Desenul din stânga prezintă un vector de deplasare, al cărui modul este de 50 km, și direcția lui formează unghi obtuz 150° cu direcția axei X. Folosind definiția, găsim proiecția deplasării pe axa X:

sx = s cos(α) = 50 km cos( 150°) = –43 km

Deoarece unghiul dintre axe este de 90°, este ușor de calculat că direcția de mișcare face un unghi ascuțit de 60° cu direcția axei Y. Folosind definiția, găsim proiecția deplasării pe axa Y:

sy = s cos(β) = 50 km cos( 60°) = +25 km

După cum puteți vedea, dacă direcția vectorului formează un unghi ascuțit cu direcția axei, proiecția este pozitivă; dacă direcția vectorului formează un unghi obtuz cu direcția axei, proiecția este negativă.

Desenul din dreapta arată vectorul viteză, al cărui modul este de 5 m/s, iar direcția formează un unghi de 30 ° cu direcția axei X. Să găsim proiecțiile:

υx = υ cos(α) = 5 m/s cos( 30°) = +4,3 m/s
υy = υ cos(β) = 5 m/s cos( 120°) = –2,5 m/s

Este mult mai ușor să găsiți proiecțiile vectorilor pe axe dacă vectorii proiectați sunt paraleli sau perpendiculari pe axele selectate. Rețineți că în cazul paralelismului sunt posibile două opțiuni: vectorul este co-direcționat către axă și vectorul este opus axei, iar în cazul perpendicularității, există o singură opțiune.

Proiecția unui vector perpendicular pe axă este întotdeauna zero (vezi sy și ay în desenul din stânga și sx și υx în desenul din dreapta). Într-adevăr, pentru un vector perpendicular pe axă, unghiul dintre acesta și axă este de 90 °, deci cosinusul este zero, ceea ce înseamnă că proiecția este zero.

Proiecția vectorului co-direcționat cu axa este pozitivă și egală cu modulul său, de exemplu, sx = +s (vezi desenul din stânga). Într-adevăr, pentru un vector co-direcțional cu axă, unghiul dintre acesta și axă este zero, iar cosinusul său este „+1”, adică proiecția este egală cu lungimea vectorului: sx = x – xo = +s .

Proiecția unui vector opus axei este negativă și egală cu modulul său, luată cu semnul minus, de exemplu, sy = –s (vezi desenul din dreapta). Într-adevăr, pentru un vector opus axei, unghiul dintre acesta și axă este de 180°, iar cosinusul său este „–1”, adică proiecția este egală cu lungimea vectorului, luată cu semn negativ: sy = y – yo = –s .

Partea dreaptă a ambelor desene arată alte cazuri în care vectorii sunt paraleli cu una dintre axele de coordonate și perpendiculari pe cealaltă. Vă invităm să vedeți singuri că în aceste cazuri sunt respectate și regulile formulate în paragrafele precedente.

1. Găsirea geometrică a proiecțiilor.

Vector
- proiectia vectorului pe axa BOU
- proiectia vectorului pe axa OY

Definiția 1. Proiecție vectorială pe orice axă de coordonate se numește un număr luat cu semnul „plus” sau „minus”, corespunzător lungimii segmentului situat între bazele perpendicularelor, coborât de la începutul și sfârșitul vectorului până la axa de coordonate.

Semnul de proiecție este definit după cum urmează. Dacă, la deplasarea de-a lungul axei de coordonate, există o mișcare de la punctul de proiecție al începutului vectorului la punctul de proiecție al sfârșitului vectorului în direcția pozitivă a axei, atunci proiecția vectorului este considerată pozitivă. . Dacă - este opus axei, atunci proiecția este considerată negativă.

Figura arată că dacă vectorul este oarecum orientat opus axei de coordonate, atunci proiecția sa pe această axă este negativă. Dacă vectorul este orientat cumva în direcția pozitivă a axei de coordonate, atunci proiecția sa pe această axă este pozitivă.

Dacă vectorul este perpendicular pe axa de coordonate, atunci proiecția sa pe această axă este egală cu zero.
Dacă un vector este co-direcționat cu o axă, atunci proiecția sa pe această axă este egală cu modulul vectorului.
Dacă vectorul este opus axei de coordonate, atunci proiecția sa pe această axă este egală în valoare absolută cu modulul vectorial, luat cu semnul minus.

2. Definiția cea mai generală a unei proiecții.

Dintr-un triunghi dreptunghic ABD: .

Definiția 2. Proiecție vectorială pe orice axă de coordonate se numește număr egal cu produsul dintre modulul vectorului și cosinusul unghiului format de vector cu direcția pozitivă a axei de coordonate.

Semnul proiecției este determinat de semnul cosinusului unghiului format de vectorul cu direcția pozitivă a axei.
Dacă unghiul este ascuțit, atunci cosinusul are semn pozitiv, iar proiecțiile sunt pozitive. Pentru unghiurile obtuze, cosinusul are semn negativ, deci în astfel de cazuri proiecțiile pe axă sunt negative.
- deci pentru vectorii perpendiculari pe axa, proiectia este zero.

Vor exista și sarcini pentru o soluție independentă, la care puteți vedea răspunsurile.

Concept de vector

Înainte de a afla totul despre vectori și operațiunile pe ei, acordați-vă pentru a rezolva o problemă simplă. Există un vector al întreprinderii tale și un vector al abilităților tale inovatoare. Vectorul antreprenoriatului te conduce la Scopul 1, iar vectorul abilităților inovatoare - la Scopul 2. Regulile jocului sunt de așa natură încât să nu te poți deplasa în direcțiile acestor doi vectori deodată și să atingi două obiective deodată. Vectorii interacționează sau, vorbind matematic, se efectuează o operațiune asupra vectorilor. Rezultatul acestei operațiuni este vectorul „Rezultat”, care vă conduce la Obiectivul 3.

Acum spuneți-mi: rezultatul cărei operațiuni pe vectorii „Întreprindere” și „Abilități inovatoare” este vectorul „Rezultat”? Dacă nu poți spune imediat, nu te descuraja. Pe măsură ce studiezi această lecție, vei putea răspunde la această întrebare.

După cum am văzut mai sus, vectorul vine în mod necesar dintr-un punct Aîn linie dreaptă până la un punct B. În consecință, fiecare vector are nu numai o valoare numerică - lungime, ci și o direcție fizică și geometrică. Din aceasta se derivă prima, cea mai simplă definiție a unui vector. Deci, un vector este un segment direcționat care merge dintr-un punct A până la punctul B. Este marcat astfel:

Și să încep altfel operații vectoriale , trebuie să ne familiarizăm cu încă o definiție a unui vector.

Un vector este un fel de reprezentare a unui punct care trebuie atins dintr-un punct de plecare. De exemplu, un vector tridimensional este de obicei scris ca (x, y, z) . Mai simplu spus, aceste numere reprezintă cât de departe trebuie să mergi în trei direcții diferite pentru a ajunge la obiect.

Fie dat un vector. în care X = 3 (mâna dreaptă arată spre dreapta) y = 1 (mâna stângă arată înainte) z = 5 (sub punct există o scară care duce sus). Din aceste date, vei găsi punctul mergând 3 metri în direcția indicată de mâna dreaptă, apoi 1 metru în direcția indicată de mâna stângă, iar apoi te așteaptă o scară și, urcând 5 metri, vei găsi în sfârșit. tu însuți la punctul final.

Toți ceilalți termeni sunt perfecționări ale explicației prezentate mai sus, necesare pentru diferite operații pe vectori, adică pentru rezolvarea problemelor practice. Să trecem prin aceste definiții mai riguroase, insistând asupra problemelor tipice vectoriale.

Exemple fizice Mărimile vectoriale pot fi deplasarea unui punct material care se mișcă în spațiu, viteza și accelerația acestui punct, precum și forța care acționează asupra acestuia.

vector geometric reprezentat în spațiu bidimensional și tridimensional în formă segment dirijat. Acesta este un segment care are un început și un sfârșit.

Dacă A este începutul vectorului și B- capătul său, atunci vectorul este notat cu simbolul sau unul literă mică. În figură, sfârșitul vectorului este indicat printr-o săgeată (Fig. 1)

Lungime(sau modul) a unui vector geometric este lungimea segmentului care îl generează

Cei doi vectori sunt numiți egal , dacă pot fi combinate (când direcțiile coincid) prin translație paralelă, adică. dacă sunt paralele, punctează în aceeași direcție și au lungimi egale.

În fizică, este adesea luat în considerare vectori fixați, dat de punctul de aplicare, lungime și direcție. Dacă punctul de aplicare al vectorului nu contează, atunci acesta poate fi transferat, păstrând lungimea și direcția în orice punct din spațiu. În acest caz, vectorul este numit gratuit. Suntem de acord să luăm în considerare numai vectori liberi.

Operații liniare pe vectori geometrici

Înmulțiți un vector cu un număr

Produs vectorial pe număr Un vector se numește vector obținut dintr-un vector prin întindere (la ) sau micșorare (la ) ori, iar direcția vectorului este păstrată dacă , și inversată dacă . (Fig. 2)

Din definiție rezultă că vectorii și = sunt întotdeauna situați pe una sau drepte paralele. Astfel de vectori se numesc coliniare. (De asemenea, puteți spune că acești vectori sunt paraleli, dar în algebra vectorială se obișnuiește să spuneți „coliniar”.) Este adevărat și invers: dacă vectorii și sunt coliniari, atunci ei sunt legați prin relația

Prin urmare, egalitatea (1) exprimă condiția de coliniaritate a doi vectori.

Adunarea și scăderea vectorului

Când adăugați vectori, trebuie să știți asta sumă vectori și se numește vector al cărui început coincide cu începutul vectorului, iar sfârșitul coincide cu sfârșitul vectorului, cu condiția ca începutul vectorului să fie atașat la sfârșitul vectorului. (Fig. 3)

Această definiție poate fi distribuită pe orice număr finit de vectori. Lăsați în spațiu dat n vectori liberi. Când se adună mai mulți vectori, suma lor este luată ca vector de închidere, începutul căruia coincide cu începutul primului vector și sfârșitul cu sfârșitul ultimului vector. Adică, dacă începutul vectorului este atașat la sfârșitul vectorului, iar începutul vectorului la sfârșitul vectorului etc. și, în sfârșit, până la sfârșitul vectorului - începutul vectorului, apoi suma acestor vectori este vectorul de închidere , al cărui început coincide cu începutul primului vector și al cărui sfârșit coincide cu sfârșitul ultimului vector . (Fig. 4)

Termenii se numesc componente ale vectorului, iar regula formulată este regula poligonului. Este posibil ca acest poligon să nu fie plat.

Când un vector este înmulțit cu numărul -1, se obține vectorul opus. Vectorii și au aceeași lungime și direcții opuse. Suma lor dă vector nul, a cărui lungime este zero. Direcția vectorului nul nu este definită.

În algebra vectorială, nu este nevoie să se ia în considerare separat operația de scădere: a scădea un vector dintr-un vector înseamnă a adăuga vectorul opus la vector, i.e.

Exemplul 1 Simplificați expresia:

.

,

adică vectorii pot fi adunați și înmulțiți cu numere în același mod ca polinoamele (în special, de asemenea, probleme pentru simplificarea expresiilor). De obicei, nevoia de a simplifica expresii similare liniar cu vectori apare înainte de a calcula produsele vectorilor.

Exemplul 2 Vectorii și servesc drept diagonale ale paralelogramului ABCD (Fig. 4a). Exprimați în termeni de și vectorii , , și , care sunt laturile acestui paralelogram.

Soluţie. Punctul de intersecție al diagonalelor unui paralelogram bisectează fiecare diagonală. Lungimile vectorilor solicitați în starea problemei se găsesc fie ca jumătate din sumele vectorilor care formează un triunghi cu cei doriti, fie ca jumătate din diferențe (în funcție de direcția vectorului care servește drept diagonală), sau, ca și în ultimul caz, jumătate din suma luată cu semnul minus. Rezultatul sunt vectorii necesari în starea problemei:

Există toate motivele să credem că acum ați răspuns corect la întrebarea despre vectorii „Întreprindere” și „Abilități inovatoare” de la începutul acestei lecții. Răspuns corect: acești vectori sunt supuși unei operații de adunare.

Rezolvați singur problemele pe vectori și apoi uitați-vă la soluții

Cum se află lungimea sumei vectorilor?

Această problemă ocupă un loc special în operațiile cu vectori, deoarece implică utilizarea proprietăților trigonometrice. Să presupunem că aveți o sarcină ca următoarea:

Având în vedere lungimea vectorilor iar lungimea sumei acestor vectori . Aflați lungimea diferenței acestor vectori.

Soluții la aceasta și alte probleme similare și explicații despre cum să le rezolvi - în lecția " Adunarea vectorială: lungimea sumei vectorilor și teorema cosinusului ".

Și puteți verifica soluția unor astfel de probleme pe Calculator online „Latura necunoscută a unui triunghi (adunare vectorială și teorema cosinusului)” .

Unde sunt produsele vectorilor?

Produsele vectoriale ori nu sunt operații pe linieși sunt considerate separat. Și avem lecții „Produsul punctual al vectorilor” și „Produsul vectorial și mixt al vectorilor”.

Proiecția unui vector pe o axă

Proiecția unui vector pe o axă este egală cu produsul dintre lungimea vectorului proiectat și cosinusul unghiului dintre vector și axă:

După cum se știe, proiecția unui punct A pe linie (plan) este baza perpendicularei coborâte din acest punct la dreapta (plan).

Fie - un vector arbitrar (Fig. 5) și și - proiecții ale începutului său (puncte A) și sfârșit (puncte B) pe axă l. (Pentru a construi proiecția unui punct A) trage direct prin punct A plan perpendicular pe dreapta. Intersecția unei linii și a unui plan va determina proiecția necesară.

Componentă a vectorului pe axa l numit un astfel de vector situat pe această axă, începutul căruia coincide cu proiecția începutului, iar sfârșitul - cu proiecția sfârșitului vectorului.

Proiecția vectorului pe axă l numit un număr

,

egală cu lungimea vectorului component pe această axă, luată cu semnul plus dacă direcția componentei coincide cu direcția axei l, și cu semnul minus dacă aceste direcții sunt opuse.

Principalele proprietăți ale proiecțiilor vectoriale pe axă:

1. Proiecțiile vectorilor egali pe aceeași axă sunt egale între ele.

2. Când un vector este înmulțit cu un număr, proiecția lui este înmulțită cu același număr.

3. Proiecția sumei vectorilor pe orice axă este egală cu suma proiecțiilor pe aceeași axă a termenilor vectorilor.

4. Proiecția unui vector pe o axă este egală cu produsul dintre lungimea vectorului proiectat și cosinusul unghiului dintre vector și axă:

.

Soluţie. Să proiectăm vectorii pe axă l așa cum este definit în referința teoretică de mai sus. Din Fig.5a este evident că proiecția sumei vectorilor este egală cu suma proiecțiilor vectorilor. Calculăm aceste proiecții:

Găsim proiecția finală a sumei vectorilor:

Relația unui vector cu un sistem de coordonate carteziene dreptunghiulare în spațiu

Cunoștință cu Sistemul de coordonate carteziene dreptunghiulare în spațiu a avut loc în lecția corespunzătoare, de preferință deschideți-l într-o fereastră nouă.

Într-un sistem ordonat de axe de coordonate 0xyz axă Bou numit axa x, axa 0y – axa y, și axa 0z – aplica axa.

cu punct arbitrar M vector de legătură spațială

numit vector rază puncte Mși proiectați-l pe fiecare dintre axele de coordonate. Să notăm valorile proiecțiilor corespunzătoare:

Numerele x, y, z numit coordonatele punctului M, respectiv abscisă, ordonatăȘi aplicatie, și sunt scrise ca un punct ordonat de numere: M(x; y; z)(Fig. 6).

Se numește un vector de unitate de lungime a cărui direcție coincide cu direcția axei vector unitar(sau ortom) topoare. Notează prin

În consecință, vectorii unitari ai axelor de coordonate Bou, Oi, Oz

Teorema. Orice vector poate fi descompus în vectorii unitari ai axelor de coordonate:

(2)

Egalitatea (2) se numește expansiunea vectorului de-a lungul axelor de coordonate. Coeficienții acestei expansiuni sunt proiecțiile vectorului pe axele de coordonate. Astfel, coeficienții de expansiune (2) ai vectorului de-a lungul axelor de coordonate sunt coordonatele vectorului.

După alegerea unui anumit sistem de coordonate în spațiu, vectorul și triplul coordonatelor sale se determină unic unul pe celălalt, astfel încât vectorul poate fi scris sub forma

Reprezentările vectoriale în forma (2) și (3) sunt identice.

Condiția vectorilor coliniari în coordonate

După cum am observat deja, vectorii sunt numiți coliniari dacă sunt legați prin relație

Să vectori . Acești vectori sunt coliniari dacă coordonatele vectorilor sunt legate prin relație

,

adică coordonatele vectorilor sunt proporţionale.

Exemplul 6 Vectori dați . Acești vectori sunt coliniari?

Soluţie. Să aflăm raportul dintre coordonatele acestor vectori:

.

Coordonatele vectorilor sunt proporționale, prin urmare, vectorii sunt coliniari sau, ceea ce este același, paraleli.

Lungimea vectorului și cosinusurile de direcție

Datorită perpendicularității reciproce a axelor de coordonate, lungimea vectorului

este egală cu lungimea diagonalei unui paralelipiped dreptunghic construit pe vectori

și se exprimă prin egalitate

(4)

Un vector este complet definit prin specificarea a două puncte (început și sfârșit), astfel încât coordonatele vectorului pot fi exprimate în termeni de coordonatele acestor puncte.

Fie începutul vectorului în sistemul de coordonate dat să fie în punctul

iar sfârșitul este la punct

Din egalitate

Urmează asta

sau sub formă de coordonate

Prin urmare, coordonatele vectorului sunt egale cu diferențele coordonatelor cu același nume ale sfârșitului și începutului vectorului . Formula (4) în acest caz ia forma

Se determină direcția vectorului cosinus de direcție . Acestea sunt cosinusurile unghiurilor pe care le face vectorul cu axele Bou, OiȘi Oz. Să desemnăm, respectiv, aceste unghiuri α , β Și γ . Atunci cosinusurile acestor unghiuri pot fi găsite prin formule

Cosinusurile de direcție ale unui vector sunt, de asemenea, coordonatele vectorului vectorului și, prin urmare, vectorului vectorului

.

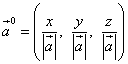
Având în vedere că lungimea vectorului vector este egală cu o unitate, adică

,

obținem următoarea egalitate pentru cosinusurile direcției:

Exemplul 7 Aflați lungimea unui vector X = (3; 0; 4).

Soluţie. Lungimea vectorului este

Exemplul 8 Puncte date:

Aflați dacă triunghiul construit pe aceste puncte este isoscel.

Soluţie. Folosind formula de lungime vectorială (6), găsim lungimile laturilor și aflăm dacă sunt două dintre ele egale:

Au fost găsite două laturi egale, deci nu este nevoie să căutați lungimea celei de-a treia laturi, iar triunghiul dat este isoscel.

Exemplul 9 Aflați lungimea unui vector și cosinusurile de direcție dacă .

Soluţie. Coordonatele vectoriale sunt date:

.

Lungimea vectorului este egală cu rădăcina pătrată a sumei pătratelor coordonatelor vectorului:

.

Găsirea cosinusurilor direcției:

Rezolvați singur problema pe vectori și apoi uitați-vă la soluție

Operații pe vectori dați sub formă de coordonate

Fie dați doi vectori și dați de proiecțiile lor:

Să indicăm acțiunile asupra acestor vectori.

În primul rând, să ne amintim ce este axa de coordonate, proiectia unui punct pe o axaȘi coordonatele unui punct de pe axă.

Axa de coordonate este o linie dreaptă căreia i se dă o direcție. Vă puteți gândi la el ca la un vector cu un modul infinit de mare.

Axa de coordonate notat cu orice literă: X, Y, Z, s, t ... De regulă, pe axă se alege (arbitrar) un punct, care se numește origine și, de regulă, este notat cu litera O. Distanțe față de alte punctele de interes pentru noi sunt măsurate din acest punct.

Proiectia unui punct pe o axa- aceasta este baza perpendicularei coborâte din acest punct spre axa dată (Fig. 8). Adică, proiecția unui punct pe axă este un punct.

Coordonată punctului pe axă este un număr, a cărui valoare absolută este egală cu lungimea segmentului axei (în scara selectată) cuprins între începutul axei și proiecția punctului pe această axă. Acest număr se ia cu semnul plus dacă proiecția punctului este situată în direcția axei de la începutul ei și cu semnul minus dacă este în sens opus.

Proiecția scalară a unui vector pe o axă- Acest număr, a cărui valoare absolută este egală cu lungimea segmentului axei (în scara selectată) cuprins între proiecțiile punctului de început și punctul final al vectorului. Important! De obicei, în locul expresiei proiecția scalară a unui vector pe o axă ei spun doar - proiecția unui vector pe o axă, adică cuvântul scalar coborât. Proiecție vectorială notat cu aceeași literă cu vectorul proiectat (în scriere normală, fără caractere aldine), cu un indice (de obicei) al numelui axei pe care este proiectat acest vector. De exemplu, dacă un vector este proiectat pe axa x A, atunci proiecția sa se notează cu x . Când proiectați același vector pe o altă axă, să spunem axa Y, proiecția sa va fi notă cu y (Fig. 9).

A calcula proiectie vectoriala pe axa(de exemplu, axa X) este necesar să se scadă coordonatele punctului de început din coordonatele punctului său final, adică

și x \u003d x k - x n.

Trebuie să ne amintim: proiecția scalară a unui vector pe o axă (sau, pur și simplu, proiecția unui vector pe o axă) este un număr (nu un vector)! Mai mult, proiecția poate fi pozitivă dacă valoarea x k este mai mare decât valoarea x n, negativă dacă valoarea x k este mai mică decât valoarea x n și egală cu zero dacă x k este egal cu x n (Fig. 10).

Proiecția unui vector pe o axă poate fi găsită și cunoscând modulul vectorului și unghiul pe care îl formează cu axa respectivă.

Figura 11 arată că a x = a Cos α

Adică, proiecția vectorului pe axă este egală cu produsul dintre modulul vectorial și cosinusul unghiului între direcția axei și direcția vectorului. Dacă unghiul este ascuțit, atunci Cos α > 0 și a x > 0, iar dacă este obtuz, atunci cosinusul unghiului obtuz este negativ, iar proiecția vectorului pe axă va fi și ea negativă.

Unghiurile numărate de pe axă în sens invers acelor de ceasornic sunt considerate pozitive, iar în direcția - negative. Totuși, deoarece cosinusul este o funcție pară, adică Cos α = Cos (− α), atunci când se calculează proiecțiile, unghiurile pot fi numărate atât în ​​sensul acelor de ceasornic, cât și în sens invers acelor de ceasornic.

La rezolvarea problemelor se vor folosi adesea următoarele proprietăți ale proiecțiilor: dacă

A = b + c +…+ d, apoi a x = b x + c x +…+ d x (în mod similar pentru alte axe),

A= m b, apoi a x = mb x (în mod similar pentru alte axe).

Formula a x = a Cos α va fi De multe ori se întâlnesc la rezolvarea problemelor, deci trebuie cunoscut. Trebuie să cunoașteți regula pentru determinarea proiecției pe de rost!

Tine minte!

Pentru a găsi proiecția unui vector pe o axă, modulul acestui vector trebuie înmulțit cu cosinusul unghiului dintre direcția axei și direcția vectorului.

Încă o dată - RAPID!

Rezolvarea problemelor privind echilibrul forțelor convergente prin construirea de poligoane de forțe închise este asociată cu construcții greoaie. O metodă universală de rezolvare a unor astfel de probleme este trecerea la determinarea proiecțiilor forțelor date pe axele de coordonate și operarea cu aceste proiecții. Axa se numește linie dreaptă, căreia îi este atribuită o anumită direcție.

Proiecția unui vector pe o axă este o valoare scalară, care este determinată de segmentul axei tăiat de perpendicularele căzute pe acesta de la începutul și sfârșitul vectorului.

Proiecția unui vector este considerată pozitivă dacă direcția de la începutul proiecției până la sfârșitul acesteia coincide cu direcția pozitivă a axei. Proiecția unui vector este considerată negativă dacă direcția de la începutul proiecției până la sfârșitul acesteia este opusă direcției pozitive a axei.

Astfel, proiecția forței pe axa de coordonate este egală cu produsul dintre modulul forței și cosinusul unghiului dintre vectorul forței și direcția pozitivă a axei.

Luați în considerare un număr de cazuri de proiectare a forțelor pe o axă:

Vector de forță F(Fig. 15) formează un unghi ascuțit cu direcția pozitivă a axei x.

Pentru a găsi proiecția, de la începutul și sfârșitul vectorului forță coborâm perpendicularele pe axă Oh; primim

1. Fx = F cosα

Proiecția vectorului în acest caz este pozitivă

Forta F(Fig. 16) este cu direcția pozitivă a axei X unghi obtuz α.

Apoi F x= F cos α, dar deoarece α = 180 0 - φ,

F x= F cosα = F cos180 0 - φ =- F cos phi.

Proiecția forței F pe axă Ohîn acest caz este negativ.

Forta F(Fig. 17) perpendicular pe ax Oh.

Proiecția forței F pe axă X zero

F x= F cos 90° = 0.

Forță situată pe un avion cum(Fig. 18), poate fi proiectat pe două axe de coordonate OhȘi OU.

Putere F poate fi împărțit în componente: F x și F y . Modulul vectorial F X egală cu proiecția vector F pe axă bou, și modulul vectorului F y este egal cu proiecția vectorului F pe axă oi.

De la Δ OAB: F x= F cosα, F x= F sinα.

De la Δ SLA: F x= F cos phi, F x= F sin phi.

Modulul de forță poate fi găsit folosind teorema lui Pitagora:

Proiecția sumei vectoriale sau a rezultantei pe orice axă este egală cu suma algebrică a proiecțiilor termenilor vectorilor de pe aceeași axă.

Luați în considerare forțele convergente F 1 , F 2 , F 3 și F 4, (Fig. 19, a). Suma geometrică, sau rezultanta, a acestor forțe F determinată de latura de închidere a poligonului de forță

Picătură de la vârfurile poligonului de forță pe axă X perpendiculare.

Având în vedere proiecțiile de forțe obținute direct din construcția finalizată, avem

F= F 1x+ F 2x+ F 3x+ F 4x

unde n este numărul de termeni ai vectorilor. Proiecțiile lor intră în ecuația de mai sus cu semnul corespunzător.

Într-un plan, suma geometrică a forțelor poate fi proiectată pe două axe de coordonate și, respectiv, în spațiu, pe trei.